|
:: 게시판
:: 이전 게시판
|
- 자유 주제로 사용할 수 있는 게시판입니다.
- 토론 게시판의 용도를 겸합니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
21/11/21 13:19
다각형의 정의를 다각형의 꼭지점을 한붓그리기로 직선으로 연결한 형태로 정의한다면 내부가 뚤린 형태의 다각형은 소거 되지 싶습니다
21/11/21 13:27
['셋 이상의 직선으로 둘러싸인 평면 도형'] 이라고 하는 것에서 직선의 정의가 어떻게 되는걸까요?
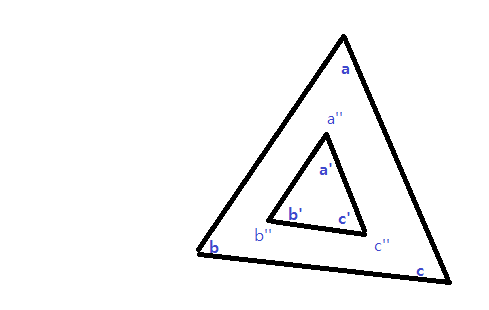
우리가 흔히 이해하는 직선의 개념이라면 삼각형 안에 삼각형을 만드는 형태의 다각형은 성립하지 않는 것 아닌가요?
21/11/21 13:29
그렇게 생각하면 오목다각형이면 무조건 다각형이 아니라는 결론이 나오고 제가 제시한 초등학교 자료에서는 선분이라고 나오므로 큰 문제가 안 된다고 봤습니다.
21/11/21 13:33
뉴비랜드 초등학교에서 막 전문적인 느낌 내 가면서 엄밀한 정의를 전체 학생들에게 가르칠 필요가 있을까 싶은데요. 나중에 0보다 작은 음수부터 허수 복소수 막 나온다고 애기들한테 그런거 먼저 가르치지 않는 것처럼요.
21/11/21 13:39
음수, 허수 복소수는 수학 수준이 올라가면서 배우는 자연스러운 확장에 가깝지만 다각형의 정의는 수준 높은 수학에서 더 엄밀하게 정의한다는 것이 새로 뭘 배우는 것을 의미하는 것이 아니라고 봐서 이야기가 다르다고 봅니다.
21/11/21 13:55
그건 다 아는 사람 입장이나 궁금해하는 사람 입장에서 그런 거고 대다수는 뭔소리여 복잡하고 짜증나게 라고 생각할 것 같은 느낌이 잔뜩 듭니다.. 맞고 틀리고의 문제가 아니구요
21/11/21 14:07
(수정됨) 자연수조차 엄밀하게 할려면 페아노 공리계나 공리적 집합론 그리고 해석학 같은거 꺼내야하는데 두리뭉실하게 대충 사과 한개 이런식으로 퉁치는데요 뭐...
그 뒤로는 고등학교때까지도 엄밀하게 하기보단 대충 느낌 알지 이 수준일텐데... 음수개념은 18-19세기까지 수학자내에서조차 받아드리지 못했던 애고...그런 자연스러운 확장조차 이해하고 받아드리기 힘든걸... 고차원적으로 정의하면 뉴비들이 잘도 알아먹겠네...
21/11/21 17:55
고딩때 배우는 극한 정의도 입실론-델타없이 대충 배웁니다. 어차피 제대로 된 학문은 대학에서부터 시작하는 것이므로 틀리지만 않으면 중등교육에선 적당히 직관만 잡아주면 충분합니다.
21/11/21 13:39
단일폐곡선의 개념을 다각형의 정의에 쉽게 녹여내면 좋을 것 같은데, 위 댓글처럼 한붓그리기 개념을 사용하면 좋을 것 같군요. 하지만 초등학교 수준의 정의라는 게 다 구멍이 있죠. 개념을 이해시키려는 과정이니 너무 엄밀함을 고집할 필요는 없는 듯 합니다.
21/11/21 14:29
참고로 초등 2학년 때 원의 개념을 배우는데, 이때 사용하는 방법은 원 그림을 그려주고 "그림과 같이 동그란 모양의 도형"이라고 설명합니다. 한 점에서 같은 거리에 있는 점들의 집합 같은 개념이 쉬워보이지만 초등학생에게는 외계어죠. 엄밀함보다는 직관적 이해가 중요한 단계인걸요.
21/11/21 13:40
뉴턴의 제 2법칙과 슈뢰딩거 방정식을 엮어서 중학생도 이해할 수 있을만큼 엄밀하고 쉽게 정의할 수 있을까요?
그게 안되니까 순차대로 가르치는 거지요.
21/11/21 13:53
직선과 평면 도형이라는 개념도 차원이나 시공간 왜곡에 따라 달라질텐데 이걸 뭐 어떻게 해야 초등학생 수준에서도 이해할 수 있는 명확한 정의가 가능할까요
21/11/21 13:58
그 이전의 교과과정에서 배우는게, 평면은 유클리드 평면, 다각형은 단일폐곡선, 볼록다각형에 국한되기 때문에 저렇게 가르쳐도 "되는"거죠. 그렇다고 아직 유클리드 평면의 개념도 제대로 습득하지 못한 학생들에게 상위 개념을 가르치는건 어렵잖아요. 수학전공자들도 어려워하는게 위상수학, 토폴로지인데 그걸 중고등학교 교과과정에 넣을수도 없는일이고요.
21/11/21 14:06
본래 수학에서 잘 정의하는건 쉬운 문제가 아닙니다.
다각형은 비교적 쉬운 편에 속합니다. 학생들에게 엄밀하게 가르쳐야하느냐는 별도의 문제이긴 합니다만. 유한 선분 유한개를 이어 만들어 단순 폐곡선이 되고 볼록인 평면 도형을 다각형이라고 하면 대체로 교과과정에서 다루는 대상에 부합합니다. 하지만, 다각형을 조금만 확장한 다면체의 경우만 보더라도 훨씬 양상이 복잡해져서 어디까지를 다면체로 해야할지 전문수학자들 사이에서도 공통된 합의가 없다고 알고 있습니다.
21/11/21 14:18
사람이 위상학적으로 도넛이랑 손잡이 달린컵이랑 같다는 말을 애들부터 알도록 가르치지 않는다면 틀린 수학교육이 되는걸까요?(손잡이가 없으면 다른 위상이라고 하더라고요)
엘빈토플러 형이 제3의 물결에서였나? 공교육의 시작은 공장식 산업체계에 근로할 노동자를 길러내는 목적으로 만들어져 있다는 식으로 말한 기억이 나네요 그러면 선생님은 저 교육을 통해 일반인을 어떤 존재로 만들고 싶으신 걸까요?
21/11/21 14:18
다각형 뿐만아니라 수많은 수학의 정의라는건 애초 초등학생이 보고듣고 이해할 정도로 만만한 개념들이 아닙니다.
그냥 사칙연산, 자연수 정수 복소수 등등도 전문수학영역으로 들어가면 논문급으로 정의가 복잡해지는게 부지기수인데 왜 그정도까지 어려운 문제를 초등학생들에게 가르쳐야 합니까? 적당히 이해하고 일상생활테 문제가 없는 정도로만 가르치는게 초등교육이 가지는 의미인데 님이 요구하는 정의의 개념은 초등학생들에게는 아무짝에도 쓸모가 없습니다.
21/11/21 14:43
제가 볼때에는 교육이란 무엇인가를 먼저 정의 하셔야 할것 같습니다.
유치원생에게 사람은 왜 사는가? 혹은 태아는 사람인가? 와 같은 개념을 이해시킬 수는 없죠.
21/11/21 15:01
일단 유클리드 기하학이 뭔지부터 엄밀히 가야죠...
초등학교때는 이게 유클리드 기하학에서 나오는지도 모르는데... 아니 유클리드가 사람이름인지 아닌지도 모를텐데 들어본적이 없어서...
21/11/21 15:27
글쓴분 논리대로라면 1이라는 숫자의 정의부터 고민해야 하고, 1+1=2라는 개념도 다시 정립해야 하는데...
수학 자체가 소멸되고 말겠네요
21/11/21 20:08
수학교육학에서 가장 먼저 배웠던 라카토스의 준경험주의 관점으로 오일러 법칙을 증명하는 과정이 생각나네요. 오일러 법칙의 반례인 구멍뚫린 다면체를 설명하기 위해 다면체의 정의를 바꾸거나, 혹은 다면체를 세분화하는 등 다양한 방법을 쓰는 걸로 기억하는데, 대학생때도 이 내용 이해 못하는 사람들이 많았던걸 생각하면 초등학교에 위의 논의를 도입하는건 결코 바람직하지 않다고봅니다..
21/11/21 21:49
공간적으로 생각해서
볼록한 공간의 다각형이나 오목한 공간의 다각형을 생각했네요. [지구 지면에 큰 삼각형을 그리면 평면상에서는 내각합이 180도 이하라던가..]
|
||||||||||