:: 게시판

:: 이전 게시판

- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다.
통합 규정을 준수해 주십시오. (2015.12.25.)

Date	2023/06/24 01:56:45
Name	묵리이장
File #1	temp.png (35.7 KB), Download : 508
Subject	[질문] 수학 문제 하나만 풀어주세요~
https://pgr21.net./qna/171308 삭게로! 점 O는 xy 좌표 평면의 원점. xy평면에서 네 개의 점 A(1,0), B(1,1), C(2,1), D(3,1) C에서 시작하여 OA 선의 한 점을 통과하고, OB 선의 한 점을 통과하여 다시 D에서 끝나는 선의 최소 길이를 구하는 문제입니다. 점들의 위치를 바꾸어 직선형으로 그려보려 하는데 영 안구해지네요.

통합규정 1.3 이용안내 인용

"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.
법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."

따닥

해시 아이콘

23/06/24 02:17

3루트2?

hodduc

해시 아이콘

23/06/24 02:23

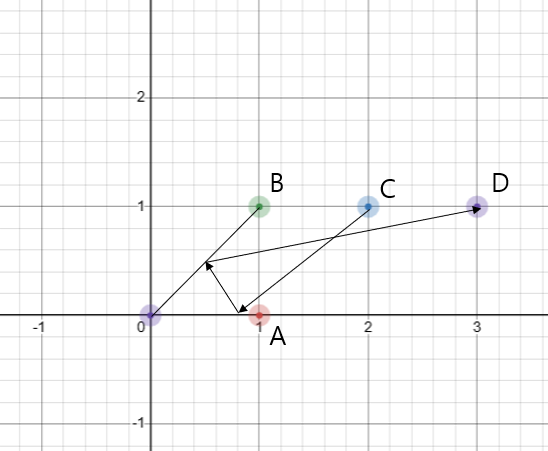
(수정됨) D를 직선 y=x에 대하여 대칭인 점 D` (1,3) 으로 바꿔도 같은 문제가 되는데요. (OB 사이의 답이 되는 점을 Z라고 하면 ZD=ZD`)
C를 직선 y=0에 대하여 대칭인 점 C` (2,-1) 로 바꿔도 마찬가지로 같은 문제가 됩니다.

그러면 선분 C`D`이 답이 되어야 하는데, 문제에서 OA 사이의 점을 반드시 지나야 한다고 하면 A를 지나가는게 가장 짧을 수밖에 없습니다. 답은 선분 C`A + AD` = sqrt(5)+3 ..?
OA 바깥쪽 점을 지나도 된다고 하면 C`D` = sqrt(17) 이 아닐까 싶네요~

EagleRare

해시 아이콘

23/06/24 02:28

동의합니다. 다만 숫자는 sqrt(2) + 3 인 것 같아요.
좌표 정해서 울프람알파에 넣어보니 같은 답이 나오긴 합니다.
https://www.wolframalpha.com/input?i2d=true&i=minimum+of+Sqrt%5BPower%5B2-a%2C2%5D%2B1%5D%2BSqrt%5BPower%5Bb-a%2C2%5D%2BPower%5Bb%2C2%5D%5D%2BSqrt%5BPower%5B3-b%2C2%5D%2BPower%5B1-b%2C2%5D%5Dwhere+0%3C%3Da%3C%3D1+and+0%3C%3Db%3C%3D1

hodduc

해시 아이콘

23/06/24 02:35

아 맞네요 (...) sqrt(5)가 어디서 나왔지.. 감사합니다!

nearby

해시 아이콘

23/06/24 07:01

점C는 x축 대칭시켜 C'(2, -1)로, 점D는 y=x 대칭시켜 D'(1,3)에 위치시킨 다음, D'A(얘가 자동으로 OB위의 점 B를 지남)+AC'을 구하면 됩니다. 3+sqrt(2)

목록 삭게로! 맨위로

번호	제목	이름	날짜	조회
172638	[질문] 마우스 추천 부탁드립니다아아 [10]	월터화이트8388	23/09/16	8388
172637	[질문] 제주에서 면세점 양주를 사려는데요 [2]	서쪽으로가자7332	23/09/16	7332
172636	[질문] 앱 개발 입문서 [2]	티타늄6411	23/09/16	6411
172635	[질문] 기사시험 실기를 준비중인데 공부를 너무 빨리(?) 마쳤습니다. [5]	WhiteBerry8284	23/09/16	8284
172634	[질문] 화장실 등이 나갔는데 냄새가 이상합니다. [3]	아밀다6671	23/09/16	6671
172633	[질문] 다급/절실] 3~4일간 알차게 마무리 가능한 게임 추천 부탁드립니다 [37]	비 평 = 이 백 만10437	23/09/15	10437
172632	[질문] 홈텍스 관련 질문 [4]	원딜은안해요6491	23/09/15	6491
172631	[질문] 3프로 네이버페이 포인트적립 또는 1.2프로 할인 어떻게 할까요? [8]	콩순이7310	23/09/15	7310
172630	[질문] 인천공항 주차 질문입니다. [9]	Nothing Phone(1)6190	23/09/15	6190
172629	[질문] 혹시 각자 쓰시는 중국어 번역기가 있다면 번역 제일 잘되는 걸로 추천해주실 수있을까요	별가느게6168	23/09/15	6168
172628	[질문] 사용중인 스마트폰 한글 자판 [77]	반대칭고양이21562	23/09/15	21562
172627	[질문] 이벌레는 이름이 무엇인가요?(사진주의) [13]	교자만두7311	23/09/15	7311
172626	[질문] 미러리스 a6700 vs r8 중에 추천 부탁드립니다. [13]	크루개7709	23/09/15	7709
172625	[질문] 넷플릭스 애니 질문입니다. [2]	하얀샤프란6369	23/09/15	6369
172623	[질문] 갤럭시 탭에서 글자체 깨져서 열리는 것 해결 방법 문의	수타군5759	23/09/15	5759
172622	[질문] PC 견적 추천 부탁드립니다. [4]	유자마카롱6537	23/09/15	6537
172621	[질문] 키와 근육의 상관관계에 대한 궁금증 [36]	시무룩7093	23/09/15	7093
172620	[질문] 일본야구 한신 우승이 어느정도인건가요? [9]	리나장6641	23/09/15	6641
172619	[질문] 일본에 대해 공부하고 싶습니다 [15]	0126양력반대7846	23/09/15	7846
172618	[질문] 라데온 7900 xtx 쓰는데 방이 너무 더워지네요. 방법이 없을까요? [7]	곰돌곰돌파트나7992	23/09/14	7992
172617	[질문] 게임 추천 좀 부탁드립니다. [23]	기대7355	23/09/14	7355
172614	[질문] 맨투맨 브랜드 추천 좀 부탁드려요. [9]	지금이대로6872	23/09/14	6872
172613	[질문] 푸쉬업바 하나로 홈트 어느정도 가능한가요? [20]	rukawa7139	23/09/14	7139

목록 이전 다음

+ : 최근 1시간내에 달린 댓글
+ : 최근 2시간내에 달린 댓글

맨 위로

PGR21.com

통합규정 1.3 이용안내 인용